机构名称:
¥ 1.0
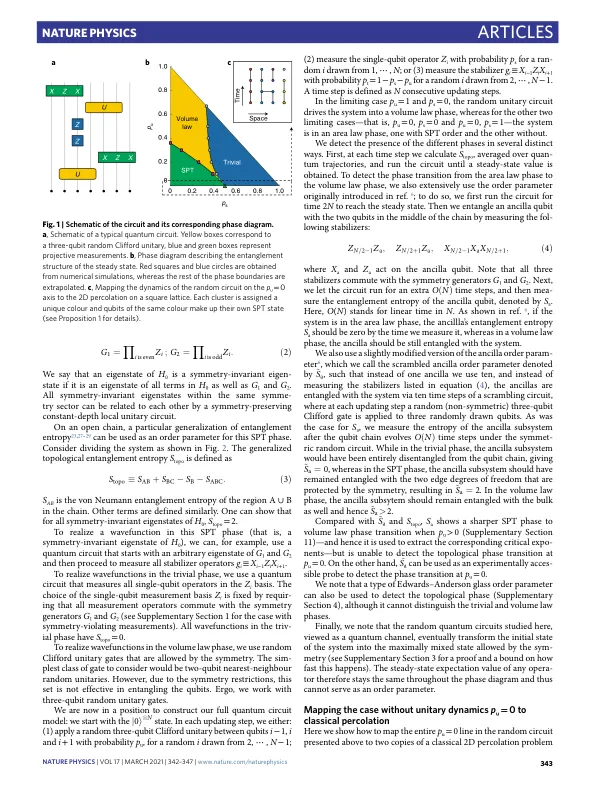
能量幺正动力学驱使量子多体系统进入高度纠缠态,其特征是子系统纠缠熵的体积定律缩放。当这种动力学被快速局部测量所拦截时,各个量子轨迹预计会坍缩为低纠缠态,其特征是子系统纠缠熵的面积定律缩放。最近发现,至少在一类模型中,这两个阶段由一个有限测量速率 1 – 3 的尺度不变的“临界点”分隔。近期,人们对这种转变及其概括的几个方面进行了研究 4 – 19 。在无限快速局部测量的极限下,系统的状态关键取决于测量基的选择。假设只测量交换的单量子比特算子,波函数就会坍缩为无纠缠的平凡积态。然而,如果选择测量一组稳定拓扑或对称保护拓扑 (SPT) 波函数的稳定算子,那么得到的状态——尽管也具有纠缠面积律标度——在拓扑上将不同于乘积状态 20 , 21 。在本文中,我们考虑这两类测量之间的竞争,以及它们与幺正动力学的竞争。这就引发了一个问题,即拓扑相的概念是否在包含幺正动力学和局部测量的随机量子电路中得到很好的定义。为了回答这个问题,我们考虑一个 (1 + 1)D 量子电路模型,它包含三个元素:(1) 稳定 Z 2 ´ Z 2 的稳定算子的测量
对称随机量子电路中测量引起的拓扑纠缠跃迁
主要关键词