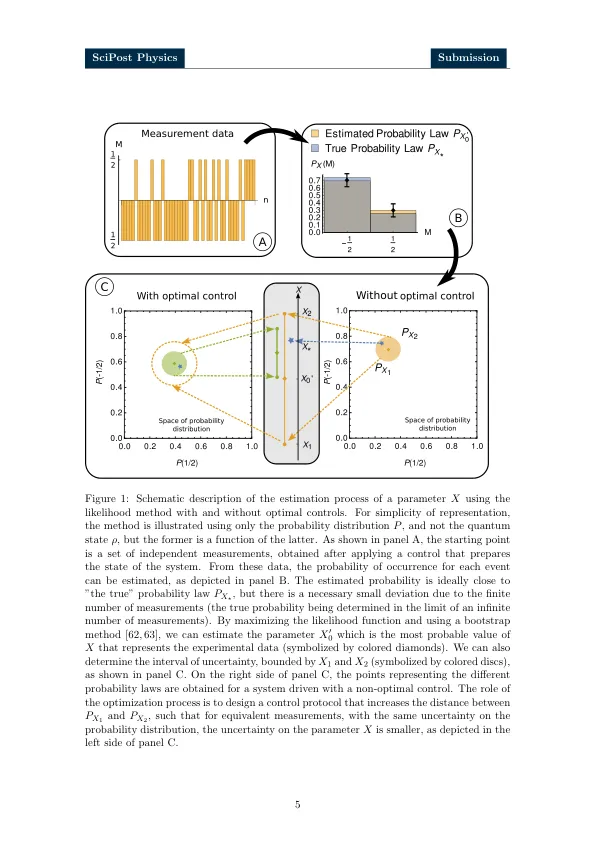
使用量子特征进行参数估计的量子计量学最近引起了人们的注意,因为它可以胜过任何基于资源的经典测量方案[1-8]。尽管可以实现令人印象深刻的精确提高,但只有在优化协议的各个步骤时才能达到最终性能[4,9,10]。标准过程通常考虑最初以最佳初始状态制备的系统的自由演变。但是,在许多示例中,这种方法还不够,并且必须通过外部控制修改系统动力学,以实现给定实验约束的最高精度。控制设计通常由最佳控制理论(OCT)执行,该理论证明了其在许多量子应用中的有效性[6,11-14]。到目前为止,已经提出了不同的解决方案,以定义最佳控制问题。它们在固定的最后时间示意性地差异以最大化(或最小化)。除其他外,我们可以提到量子渔民信息(QFI)[10,15–30],选择性控制方案[31-39]和指纹识别方法[40-43]的最大化。QFI基于与量子系统结合的cram'er-rao的概括[9,44,45]。对于纯状态,QFI与特定可观察的特定可观察的方差成正比,该方差与哈密顿量的部分衍生物相对于参数进行估计。通过最大化此数量,我们确保参数的小扰动会引起对系统动力学的显着修改,因此,这使我们能够减少测量过程中造成的误差。对于QFI,该信息在参数空间中是本地的,并且在控制问题的定义中没有明确的目标量子状态。本质上非本地的选择性控制过程并非如此。可以将它们视为以不同参数值为特征的系统的不同副本的同时状态对状态控制协议[33,34,36,46-46-50]。选择性控制已广泛用于核磁共振中[51-55]。在此框架中,目标是找到一个控制系统的控件,以达到系统的每个副本,以达到(可能尽可能快)的目标状态,并专门选择目标状态以最大程度地减少测量误差。指纹方法更加详尽,并结合了来自QFI和选择性协议的想法[40-43]。没有特定的目标状态,但目标是最大化一个或几个可观察到的时间演变之间的距离。在这种情况下,考虑了整个动态,而不仅仅是最终系统配置[43]。除了给定优点的最大化外,还可以包括其他约束来分析这些问题,例如控制时间或能量的最小化[56-59]。可以通过这些方法独立地获得不同的控制策略,例如,用于自旋系统的参数估计。自然出现的一个问题是在哪些条件下这些控制方案是等效的,更一般而言,不同技术之间的优点,相似性和差异。本文旨在朝这个方向迈出一步。据我们所知,只有指纹方法已短暂地连接到[60,61]中的Fisher信息,但是QFI和选择性方案之间的关系仍未得到探索。为了简化分析,我们专注于链接
量子系统参数估计的最佳控制策略
主要关键词