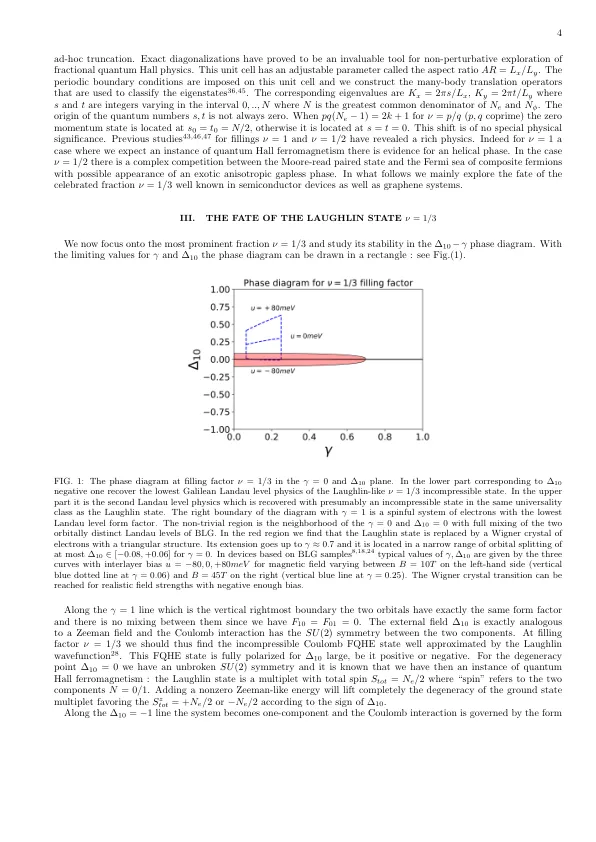
基于石墨烯的样品显示量子厅制度1-16中的相关阶段丰富。奇数和均匀的分数量子霍尔状态,在涉及石墨烯 - 己酮氮化硼的样品中已经实现了分数Chern绝缘子。同样感兴趣的是双层样品中的现场诱导的激子冷凝物。已经指出,AB堆叠(Bernal)双层石墨烯(BLG)系统具有方便的参数,可以通过实验调整:除了电子密度和外部施加的磁力纤维外,还可以进行实验调整。由于几个量子数的结合,BLG的中央兰道水平具有将近八倍的变性:普通旋转,山谷的自由度和轨道退化。这些级别中排序的模式是非常丰富而复杂的。已经表明,分数量子霍尔状态17中存在可调相变。电偏置直接控制轨道水平之间的分裂和电子之间的库仑相互作用也受到外部施加磁场的值以及偏置的影响。对整数量子厅状态进行了详细研究,已在这些系统18上进行,并表明适当的紧密结合模型可以捕获水平顺序。最近的进步导致观察到许多分数状态以及它们之间的过渡。这意味着我们可以使用一个物理系统,在该系统中,我们可以调节参数影响分数量子霍尔物理学19-27。在GAAS中的二维电子系统中,众所周知,不可压力的电子液体与电子晶体(所谓的Wigner晶体)之间存在竞争。对于最低的Landau水平的填充因子ν= 1 /3,具有库仑相互作用的电子系统的基态是一种不可压缩的液体,其特性由Laughlin波函数28很好地描述,仅针对小小的细小因素,即基态状态为晶体状态29。确定这些阶段之间的精确边界已证明了困难的问题30。晶体状态在降低温度时以纵向电阻的不同而显示为绝缘状态。当一个降低填充因子时,有实验证据是Wigner晶体重新进入的实验证据。晶体状态的研究很困难,因为破坏了分数量子霍尔液体所需的磁场值很大。晶体状态不是唯一与液态的竞争者。在较高的Landau水平上,已知电子系统还可能形成所谓的条纹或气泡相。作为Wigner Crystal,这种状态破坏了翻译对称性,并且认为它们处于截然不同的物质状态而没有拓扑顺序。他们的实验特征是具有其他各向异性特性的绝缘行为。我们注意到,在二维GAAS电子或孔系统中31–35在几个多体基础状态之间存在丰富的竞争,并且可以通过调谐门电位在1/3处稳定Wigner晶体。石墨烯系统是研究此类竞争阶段的另一个领域,特别是由于其可调性,AB堆叠了双层石墨烯。也已经知道,与较高的Landau水平混合会使竞争偏向Wigner Crystal状态。调整BLG系统以获得n = 0和n = 1特征的Landau水平的退化,可以看作是Landau级别混合的极端例子,尽管没有n>1。因此,可以调整Laughlin State和Wigner Crystal之间的竞争是合理的。在本文中,我们研究了对填充因子ν= 1 /3和ν= 2 /3发生的不可压缩量子霍尔的状态,当系统完全山谷以及在AB堆叠的双层石墨烯系统中旋转极化。有趣的物理学现在是从轨道特征n = 0和n = 1的水平的穿越中出现的。根据目前对级别订购的知识,这应该发生在接近ν= - 3的载荷的中心八位。电子形成一个有效的两个组件系统,具有可调的各向异性相互作用。
Bernal Birayer石墨烯中竞争的Laughlin State和Wigner Crystal
主要关键词