机构名称:
¥ 3.0
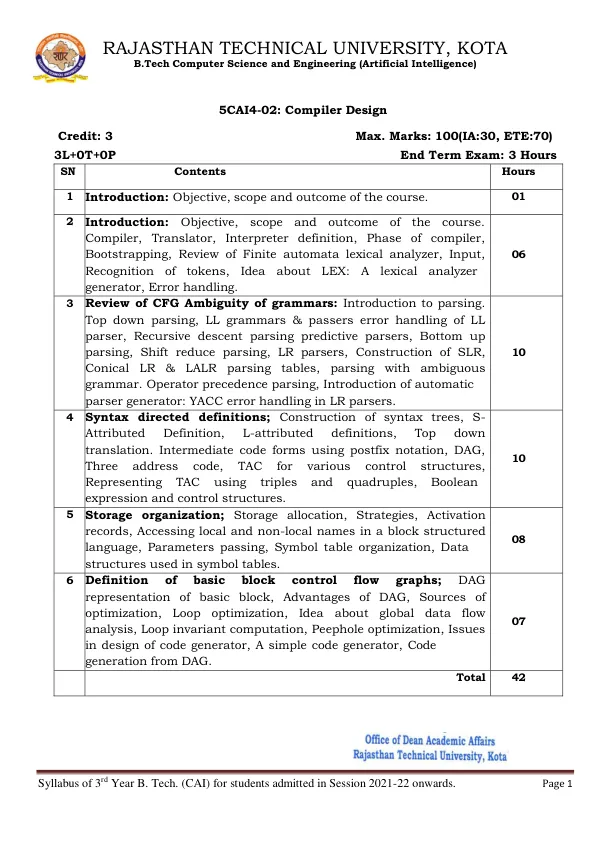
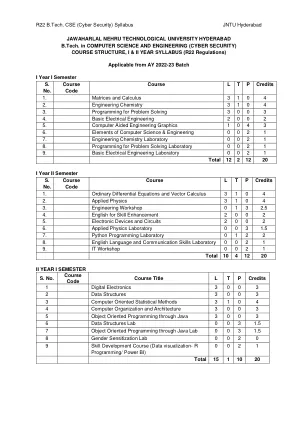
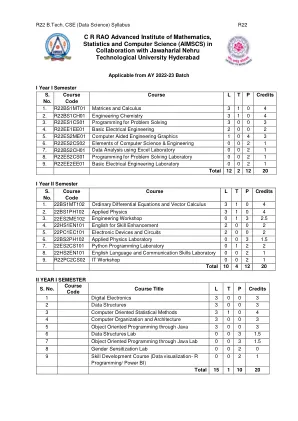
课程目标:1. 介绍各种数学概念和模型,并提供实施这些模型所需的技能。2. 对各种数值和数据进行批判性评估。3. 培养对非确定性问题建模的设计技能。预期课程成果:1. 展示对数据科学中与线性代数、概率和微积分相关的基本数学概念的理解并运用它们。 2. 应用线性模型进行回归,使用线性模型进行分类 3. 采用核模型、SVM 和 RVM 4. 将问题概念化为图模型、混合模型,并使用估计最大化算法进行分析 5. 用说明性例子进行演示 PCA 单元:1 线性代数 3 小时 矩阵、求解线性方程、向量空间、线性独立性、基和秩、线性映射、仿射空间、范数、内积、正交性、正交基、函数内积、正交投影 单元:2 矩阵分解 4 小时 行列式和迹、特征值和特征向量、Cholesky 分解、特征分解、奇异值分解、矩阵近似 单元:3 向量微积分 4 小时 单变量函数的微分、偏微分和梯度、向量值函数的梯度、矩阵的梯度、计算梯度的有用恒等式、反向传播和自动微分、高阶导数、线性化和多元泰勒级数。单元:4 概率、分布和优化 4 小时 概率空间的构建、离散和连续概率、求和规则、乘积规则和贝叶斯定理、汇总统计和独立性、高斯分布、共轭和指数族、变量变换/逆变换、连续优化、使用梯度下降的优化、约束优化和拉格朗日乘数、凸优化单元:5 数据模型 4 小时 数据、模型和学习、经验风险最小化、参数估计、概率建模和推理、有向图模型、模型选择
课程大纲第三年 CSE(AI) V & VI 学期..pdf
主要关键词