机构名称:
¥ 1.0
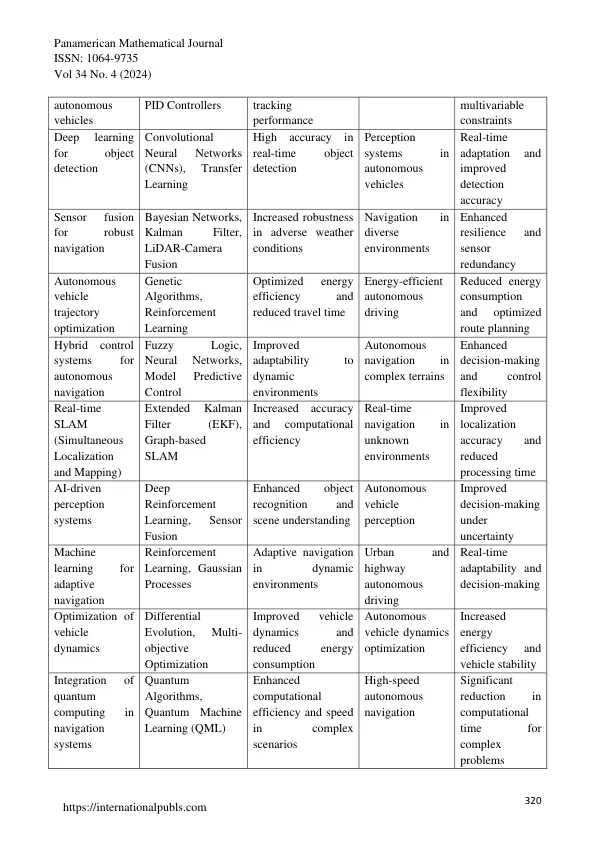
摘要:高级数学方法在自动驾驶指导系统中经常使用,以确保它们正常,可靠和有效地工作。这个摘要谈论用于创建和改进这些系统的一些最重要的数学方法。一种重要的方法是概率机器人,它使用贝叶斯过滤器,例如Kalman滤波器及其非线性版本(扩展的Kalman滤波器和无味的Kalman滤波器)来估计车辆的状态并了解不总是清晰或响亮的传感器数据。路径规划算法(如A和Dijkstra的算法)需要找到最佳路线。基于抽样的方法,例如快速探索随机树(RRT),可以帮助解决高维空间中的问题。控制理论是保持汽车稳定并遵循您想要采取的方向的非常重要的部分。模型预测控制(MPC)经常使用,因为它可以在考虑系统行为时处理具有多个变量的控制作业。用于建模车辆如何移动,使用微分方程和动力学系统理论来显示控制输入如何影响车辆随着时间的推移的作用。此外,将来自LiDAR,相机和GP等不同来源的数据组合在一起的方法对于制作世界的准确而完整的图片非常重要。优化方法通过调整汽车的路径,减少能源利用并缩短行程时间来改善跟踪。通过使用老式的数学方法和新的,尖端的机器学习方法,自动驾驶汽车跟踪系统变得越来越聪明,更有能力和更可靠。除了这些方法外,还越来越多地将机器学习和深度学习添加到指导系统中,以帮助他们做出更好的决策,并在快速变化且非常复杂的设置中更加灵活。这些模型可以通过查找趋势并进行预测来从非常大的数据集中学习,这些预测对于找到对象,理解场景和自行做出决策等任务很重要。这使得他们可以在现实生活中广泛使用。
自动驾驶汽车导航系统的数学技术
主要关键词