机构名称:
¥ 1.0
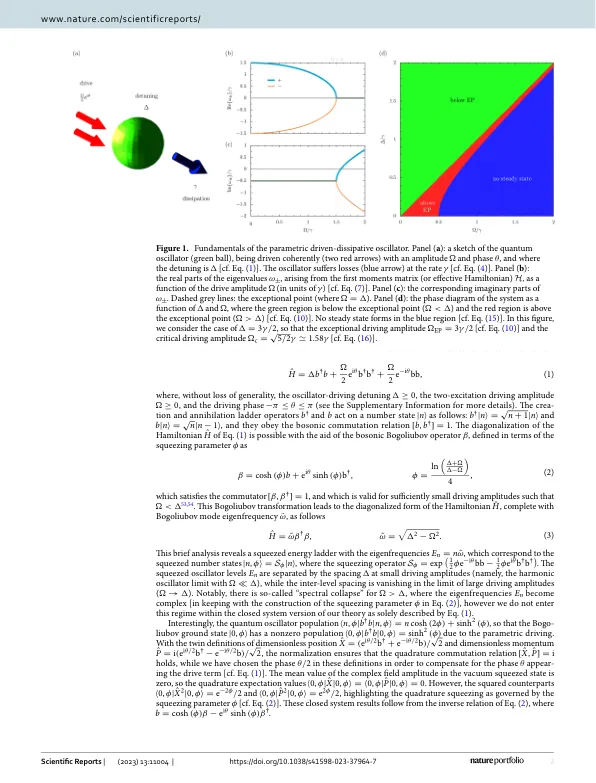
物理理论中使用的数学对象并不总是很好。爱因斯坦的时空理论允许时空的奇异性和范霍夫奇异性在凝聚的物理学中出现,而强度,相位和极化奇异性则遍布波浪物理学。在受矩阵控制的耗散系统中,奇异点出现在参数空间的特殊点上,因此某些特征值和特征向量同时合并。但是,在开放量子系统方法中描述的量子系统中产生的特殊点的性质的研究少得多。在这里,我们考虑了参数驱动的量子振荡器,并遭受损失。这个挤压系统在描述其第一矩和第二矩的动力学方程中表现出一个特殊的点,这是两个具有独特物理后果的阶段之间的边境。尤其是我们讨论种群,相关性,挤压二次和光谱如何取决于高于或低于特殊点的光谱。我们还评论临界点上存在耗散相变的存在,这与liouvillian间隙的闭合有关。我们的结果邀请了在两光子驱动器下对量子谐振器的实验探测,并且可能更广泛地重新评估了耗散量子系统内的特殊和关键点。
参数将量子振荡器驱动到异常
主要关键词