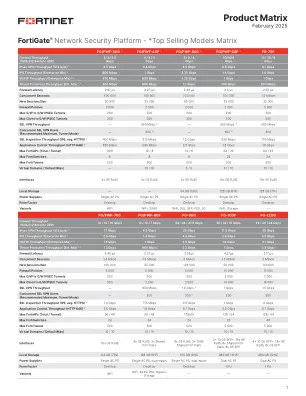
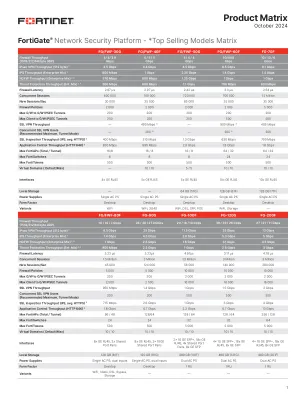
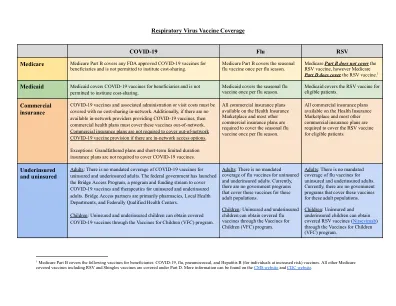
机构名称:
¥ 1.0
摘要 - 在本文中,我们研究了在通用量子游戏中学习的广泛使用矩阵乘量(MMW)动力学的平衡收敛性和稳定性。这项努力的一个关键困难是,诱导的量子状态动力学自然地分解为(i)经典的,可交换性的成分,该动态以类似于在经典复制器动力学下的混合策略的演化方式控制系统特征值的动力学; (ii)系统特征向量的非交通分量。这个非交通性的组件没有经典的对应物,因此需要引入(渐近)稳定性的新颖概念,以说明游戏量子空间的非线性几何形状。在这种一般情况下,我们表明(i)只有纯量子平衡才能稳定并在MMW动力学下吸引; (ii)作为部分匡威的纯量子状态,满足某种“变分稳定性”条件的纯量子总是会吸引。这使我们能够充分表征在MMW动力学下稳定并吸引的量子NASH平衡的结构,这一事实对预测多代理量子学习过程的结果具有重要意义。
量子游戏中矩阵倍增权重动态的稳定性
主要关键词