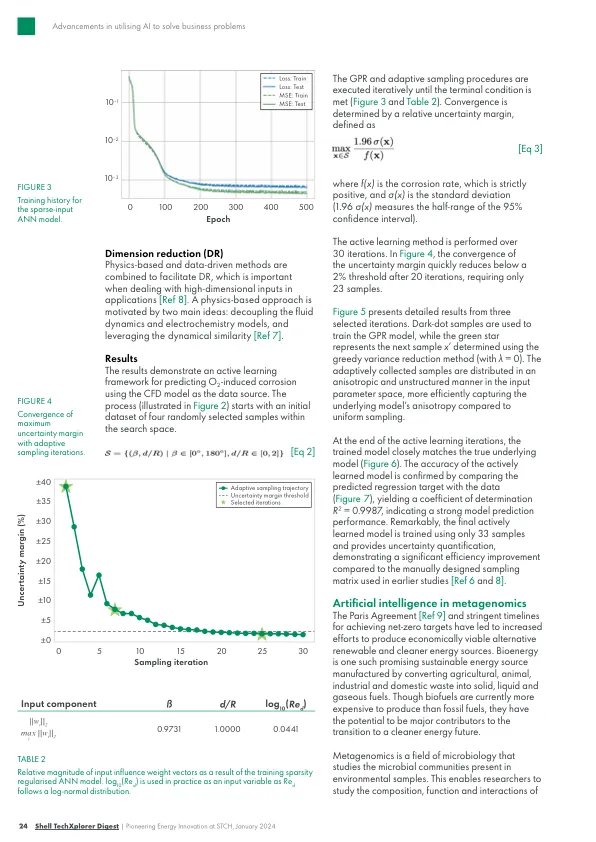
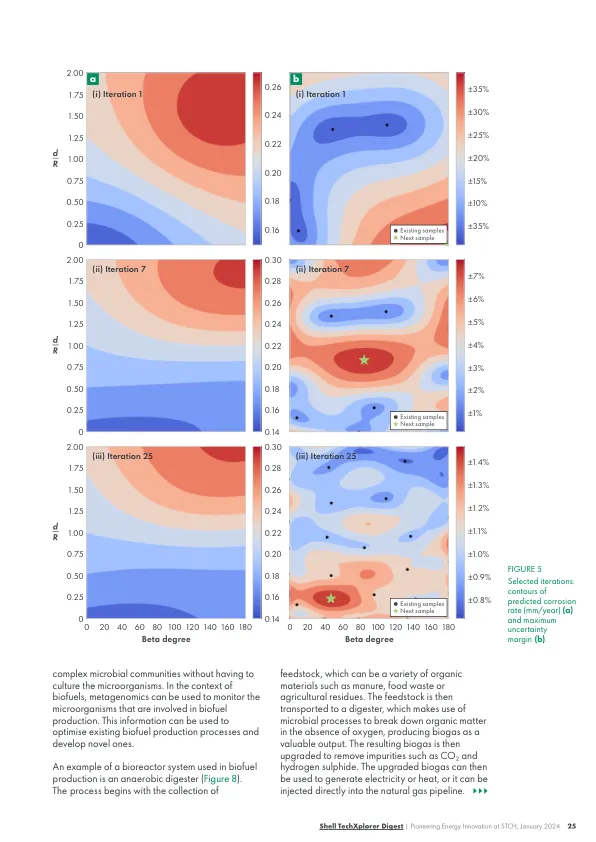
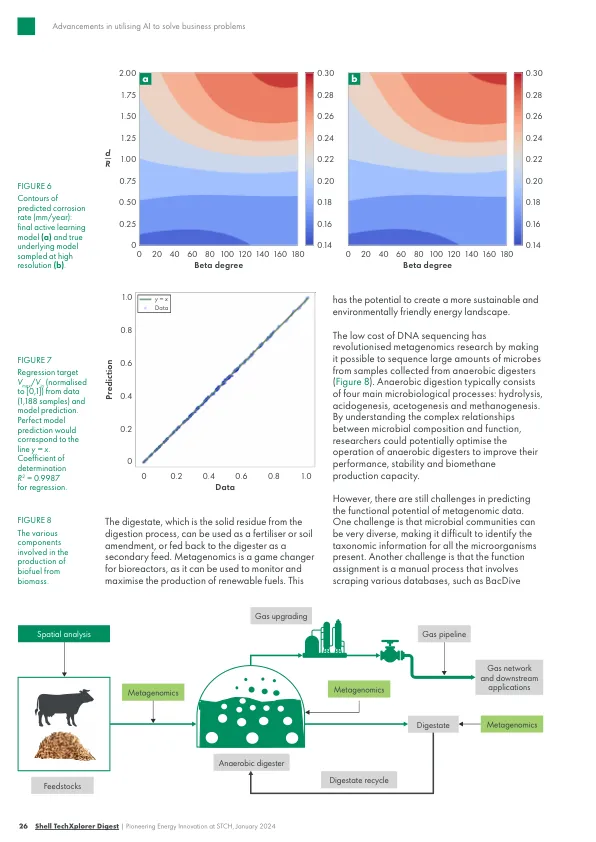
机构名称：
¥ 1.0
高斯过程回归预测模型利用 GPR 通过灵活的核来表示复杂的非线性多元函数。GPR 的贝叶斯框架量化了预测的不确定性，有助于决策并指导主动学习过程。回归使用高斯过程 (GP) 量来找到一个特定的函数分布，以解释观察到的样本 [参考文献 7]。所用特定核的 GP 模型参数 θ 对 Matérn 5/2 核的长度尺度和方差以及白噪声核的噪声水平进行编码。对于每个 GP 模型，使用最大似然估计来调整参数 θ ，以最好地解释给定的数据集 D 。GPR 的计算复杂度是时间成本的立方缩放 O(n3)，样本大小 n 归因于 K-1（相当于 n×n 密集核矩阵的逆）。为了降低复杂性，使用了降维方法。
利用人工智能解决业务问题的进步
主要关键词
相关文件推荐
