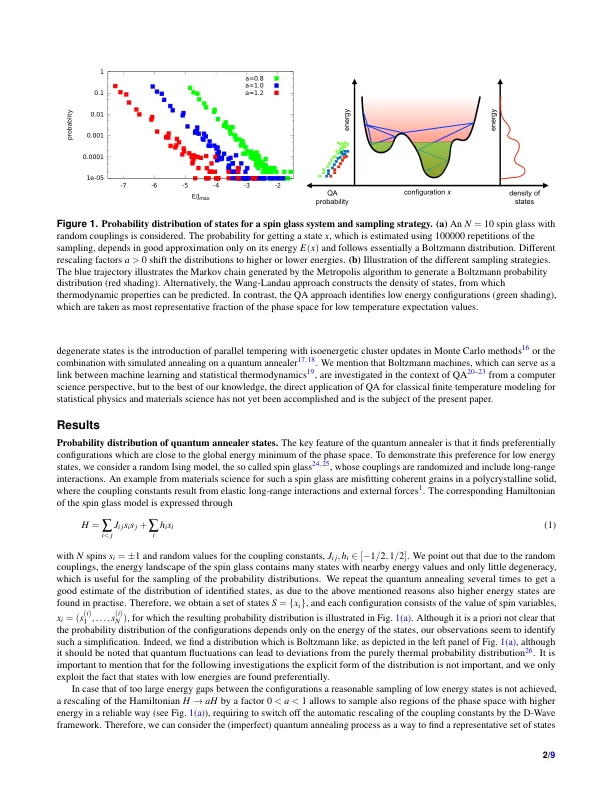
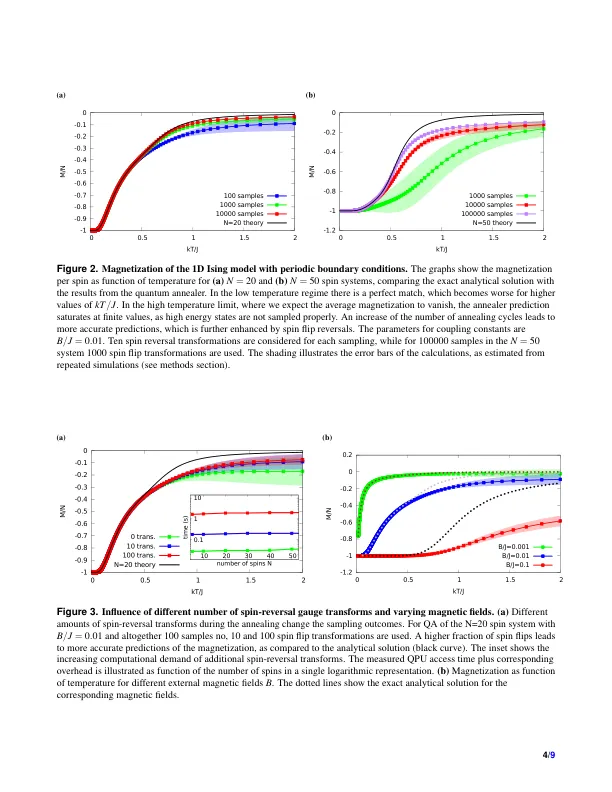
量子退火 (QA) 的出现是未来量子计算发展的重要一步,也将极大地促进统计物理和材料科学建模的发展。到目前为止,QA 在这些领域的应用仍然很少,其中包括确定具有长程弹性相互作用的平衡微结构 1 、横向场 Ising 模型中的相变 2 、通过 Shastry-Sutherland 模型研究受挫磁系统的能态 3 以及设计超材料 4 。另一个例子是结合使用量子退火器和玻尔兹曼机来采样自旋玻璃并预测 MoS 2 层的分子动力学数据 5 。更一般地说,由 D-Wave 公司实施的 QA 可以有效地找到离散优化问题的基态配置,在学术界和工业界都有许多应用 6 – 10 。 QA 的概念是在低温下以明确定义的基态初始化系统的哈密顿量,然后平滑地转换能量景观,使其代表所需的优化问题。如果仔细执行这种绝热变换,系统最终会处于目标哈密顿量的基态,因此可以找到优化问题的全局最小值。然而,在实践中,准备、转换和读出过程并不是完全绝热、无噪音和与环境分离的,因此有时会发现能量更高的状态,尤其是与简并态 11 或太小的能隙结合时。因此,对于典型的 QA 应用,需要多次重复和读出来确定真实基态。在本文中,我们证明了该技术的这一缺陷实际上可以转化为优点,因为它可以非常有效地确定有限温度的热力学性质。从材料科学的角度来看,T = 0K 时的基态配置通常只对许多实际应用具有有限的意义。例如,对于铁磁体,所有自旋都排列在基态,而对于有限温度,热涨落会导致有限的关联长度、相变和温度相关的磁化。对此类属性进行统计建模的传统方法是使用蒙特卡罗 (MC) 采样技术,因为由于相空间的巨大规模,通常无法明确计算配分函数。此类计算最突出的方法可能是使用 Metropolis 转移概率生成离散马尔可夫链,这会生成一系列遵循玻尔兹曼统计的配置,因此可以通过更容易地计算这些马尔可夫链上的时间平均值来表达集合平均值 12、13。在实践中,根据玻尔兹曼分布 p ∼ exp ( − β ∆ E ) (其中 β = 1 / k BT ),从一个状态到另一个状态的转变正在发生,其概率取决于两个配置之间的能量差 ∆ E 。通常,这种方法在低温下效率低下,因为新配置的拒绝率非常高,因此在局部最小值中捕获的相空间采样不足,导致对所需热力学性质的预测有噪声。另一种重要的采样策略是由 Wang 和 Landau 开发的,他们使用非马尔可夫算法通过平坦直方图技术提取状态密度,从中可以计算出所有所需的热力学性质 14 。除了这些主要技术之外,Dall 等人还开发了一种在低温下快速采样玻尔兹曼分布的算法。然而,这种算法最适合具有短程相互作用的系统 15 。另一种公平采样基态和
使用...进行高效低温蒙特卡洛采样
主要关键词